Digital RIAA de-/pre-emphasis filters
T.O.C.
1. EQ (VST -plug-in) w/ RIAA preset
2. Max/MSP implementation (standalone)
3. SynthMaker implementation (simple VST plug-in)
4. SynthEdit implementation (simple VST plug-in)
5. CPS implementation (simple)
External Subsonic/Rumble filtering
RIAA Filter software specs
Coefficients
Resolutions
Resolution 1. EQ (VST -plug-in) w/ RIAA preset
ddmf has couple good free EQ's you can use for this:
-
IIEQ (-> v. 1.12)
-
IIEQ 1.21 ->
-
SmallEQ
-
Morcky
Additional software, you may need
-
VST Host application (Hermann Seib's VSTHost or SAVIHost)
-
Sonalksis FreeG for additional gain if you connect the turntable w/o decent flat pre-amp
Available RIAA EQ Presets for above mentioned ddmf EQ's:
NOTE: These RIAA EQ Presets does not work correctly w/ other ddfm EQ's (meaning LP10 and IIEQ Pro) and are samplerate sensiteve (44.1kHz filter does not work @ 96kHz).
IIEQ v1.12 DISCONTINUED PRODUCT
RIAA Preset for IIEQ v. 1.12 @ 44.1kHz and 96kHz
SmallEQ
RIAA Preset for SmallEQ @ 44.1kHz
IIEQ v. 1.21 and Morcky IIEQ
RIAA Preset for IIEQ v. 1.21 @ 44.1kHz
Downloads - https://docs.google.com/file/d/0B2orKJuZJ5YOTFV6aHBkcS14RVU/edit?usp=sharing
Above 44.1kHz presets gives the RIAA curve shown red in below picture (blue is the reference curve (RIAA standard)):
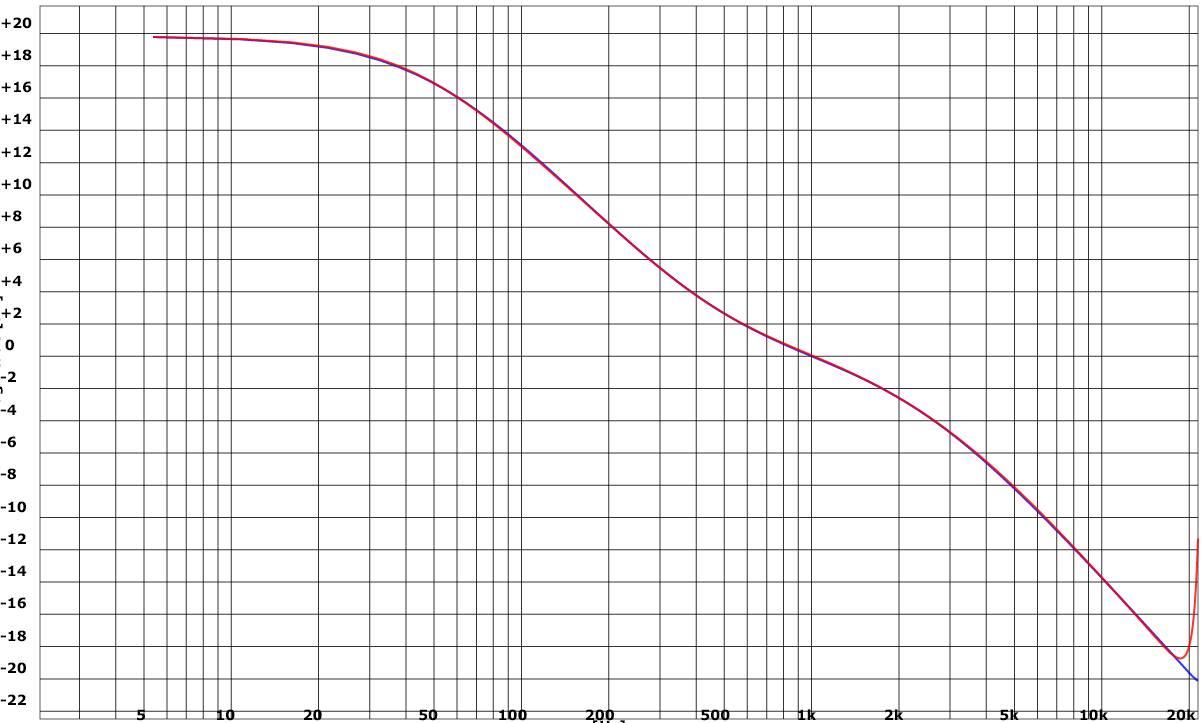
If you prefer to tweak those 44.1kHz presets to become more accurate, it's easiest to do by using Cristian Budde's Plugin Analyzer.
Quality:
The IIEQ/SmallEQ VST preset is adjusted visually by the results got from a filter build using Orbans coefficients, on VST Plugin Analyzer ... so it's basically as accurate as you be able to zoom the graph to get the curve fitted/data resolution (Hz, Q, Gain) on IIEQ/SmallEQ. It's possible to export the plot result from "VST Plug-in Analyzer" (my graphs were made w/ it) but, as it's not accurate plot (only 4096 points). I did compare the
results between a Delphi implementation of VST filter prepared using Orbans coefficients and IIEQ/SmallEQ version ... error: avg. under ±0.05dB (0Hz- ~ 18.2kHz) and from ±0.1dB to -1.6dB (~18.2kHz - 20kHz)).
Resolution 2. Max/MSP implementation
Needed components:
-
Max/MSP Runtime (or trial version)
Additional software (extract these into same directory w/ RIAA_Filter (or install using the installer)):
RIAA Filter software for Max/MSP 4.x:
for Max/MSP 5.x:
- open the RIAA_Filter.pat/.maxpat into Max/MSP enviroment
- open the I/O settings dialog and configure the driver (samplerate, latency, etc.) and I/O ports properly
- reset the Filter to defaults (Max/MSP 5.x resets to preset #1)
- select Filter samplerate (needs to be equal w/ driver samplerate)
- optional: enable subsonic filter and select the filter typw (analog/digital) (Max/MSP 5.x)
- adjust Filter Gain to ~1.0
- start the engine by pressing the Start/Stop -button
Additional options (PC):
The SPAN and Recorder can be called by pressing the Open buttons. If nothing happens, it's possible that VST .dll files needs to be
moved into same directory with the filter software. These VST's are connected parallel so the recording level can be set by the SPAN output graphics/data.
The internal Rumble/Subsonic filter is not well done (need to be fix it someday).
To edit the project file, least the trial version of Max/MSP is needed. Editing is enabled through menu option View -> Edit.
It's possible to save the project ans use it even after the trial period through Max/MSP runtime.
Issues?
If no audio ...
ASIO drivers are needed
resetting the filter to defaults or changing subsonic filter parameters (drag with mouse) can be helpful.
If still no audio or no filter added (i.e. bassless/bright audio coming out) then, maybe all connections, levels, HW monitoring state, etc. needs to be adjusted).
I found E-MU 0404 USB troublesome when changing samplerate on-the-fly. If the filter freezes, just kill the MaxRT or Max process through task manager (ctrl-alt-del).
I/O Settings:
-------------------------------------------------------------------------------------------------------------------------------------
Resolution 3. SynthMaker implementation
Download SynthMaker (NOTE: trial version adds peridiocal noise ...)
On SynthMaker enviroment, it's possible to use two different methods to build a plug-in:
1. by Coding:
// RIAA EQ Reproduction Filter for 48kHz data
monoin inL;
monoin inR;
monoout outL;
monoout outR;
float a0, a1, a2;
float b0, b1, b2;
float inL1, inL2, inR1, inR2;
float outL1, outL2, outR1, outR2;
a0= 1.00000000000000000;
a1=-0.75555209999999995;
a2=-0.16462571129709999;
b0= 1.00000000000000000; // never needed
b1=-1.73276550000000020;
b2= 0.73455344362250008;
// Proces left channel
outL = a0*inL + a1*inL1 + a2*inL2 - b1*outL1 - b2*outL2;
// Process right channel
outR = a0*inR + a1*inR1 + a2*inR2 - b1*outR1 - b2*outR2;
// save previous I/Os
outL2 = outL1;
outL1 = outL;
inL2 = inL1;
inL1 = inL;
outR2 = outR1;
outR1 = outR;
inR2 = inR1;
inR1 = inR;
2. By using build-in components:
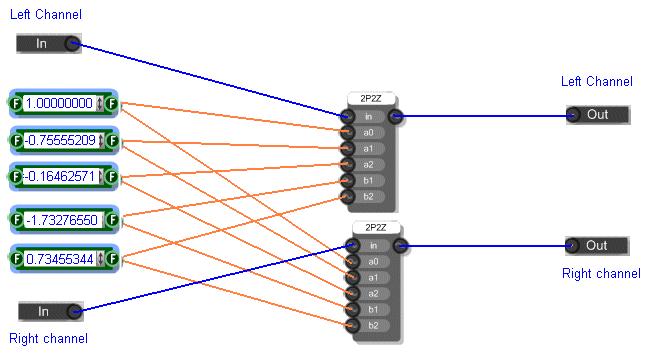
Coefficients for various filters can be found in the end of this page.
Load the RIAA EQ VST plug-in to a VST Host software etc. .
Resolution 4. SynthEdit implementation
Needed software: SynthEdit from http://www.synthedit.com/
-
David Haupt's DH_BiquadFilter SE -module (for RIAA filter) from http://www.dehaupt.com/SynthEdit/DH_BasicModulePak.htm
-
Christian W. Buddes Butterworth or Chebyshev LP/HPFilter module (for Subsonic filter) from http://www.savioursofsoul.de/Christian/?page_id=442
- extract these SE -modules to a specific folder under SynthEdit installation folder (i.e. \Program Files\SynthEdit\modules\<name>)
- if you have SE running already, it's needed to restart to get the new modules recognized.
-
SynthEdit project files - https://docs.google.com/file/d/0B2orKJuZJ5YOTFV6aHBkcS14RVU/edit?usp=sharing
- extract SynthEdit project files somewhere you find them easily (\Program Files\SynthEdit)
You may also need to make a folder named as ”vstplugins” under \Program Files\SynthEdit\.
Save SE project as a VST plug-in:
It's needed to create separate plug-in for each samplerate (44.1/48/88.2/96kHz and 192kHz) so, I have made four separate projects because of that (to make it simple).
Start SynthEdit and load the project file (riaa_se_xxx.se1) you want to save as VST plug-in.
Something like this should appear:
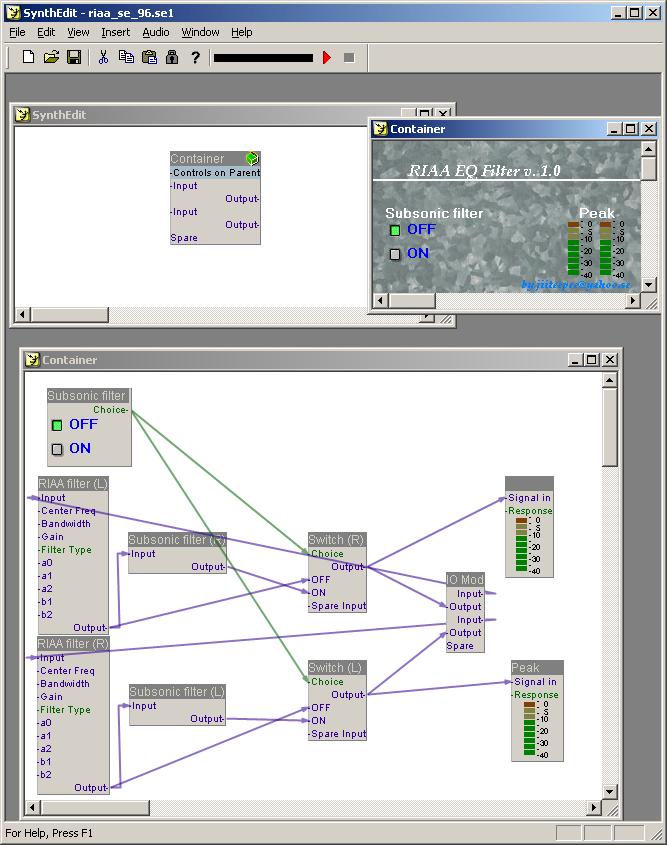
From File -menu, select Save as VST...
Name the .dll file and give an unique ID for each plug-in you create.
NOTES:
-
It's possible to change RIAA filter gain by modifying filter coefficients a0, a1 and a2 by either multiplying (increase gain) or
dividing (decrease gain) them using same multiplier/divider.
- select the DH_BiquadFilter, mouse_right_click and then select Properties
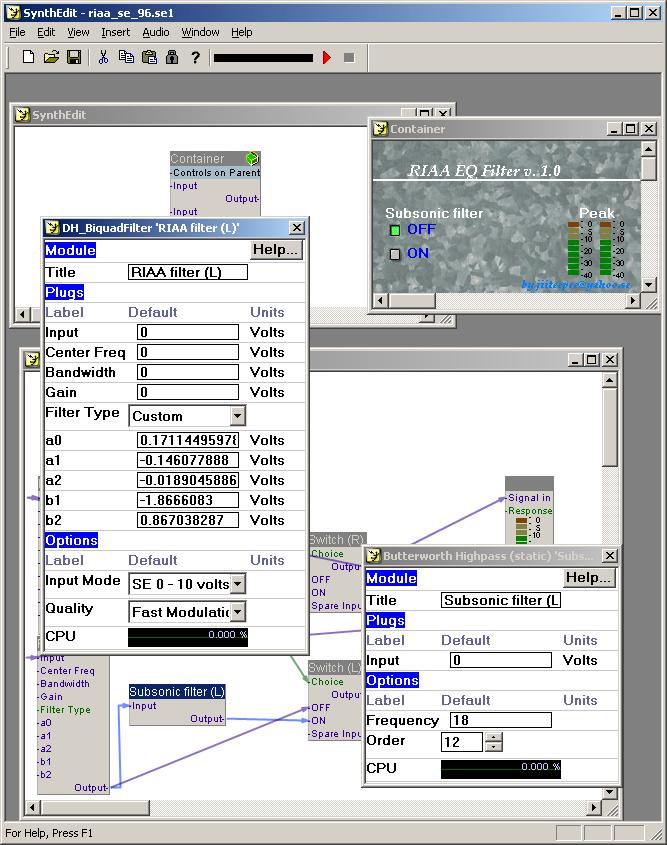
- enter new coefficients (be careful w/ values, separator (dot) and signs (+/-))
- it's needed to modify both filters (Right/Left channels, both uses equal coefficients)
- do not change coefficients b1 and b2 !!
subsonic filter order and frequency can be changed aswell
Load the RIAA EQ VST plug-in to a VST Host software etc. .
Subsonic filter result:
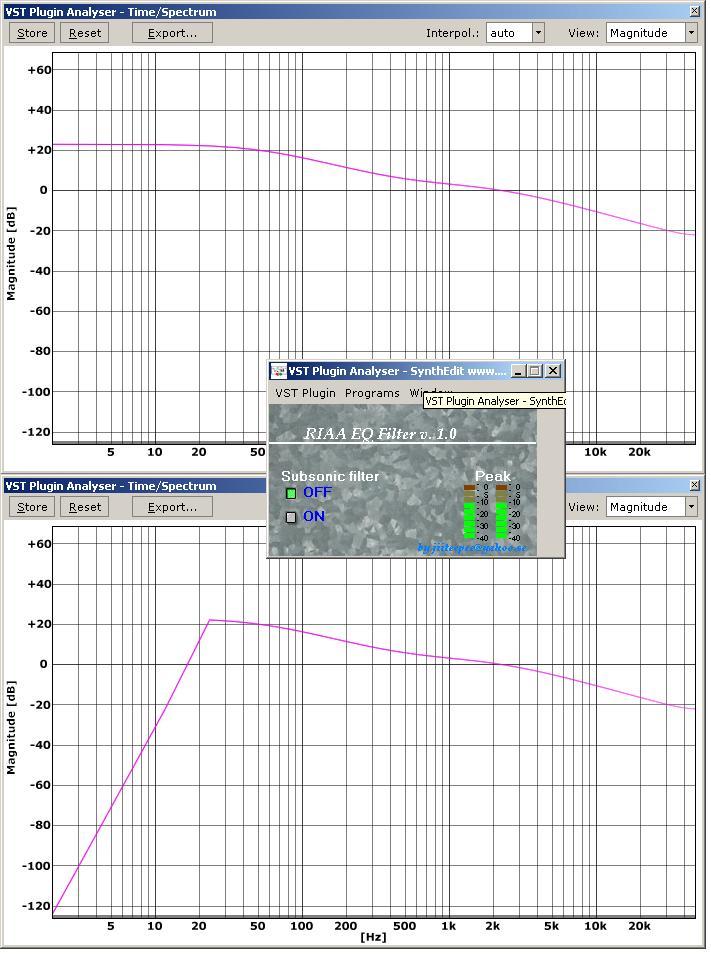
NOTE:
Resolution 5. CPS implementation
<not implemented>
To use for SUBSONIC/RUMBLE Filtering
Aixcoustic Creation's Electri-Q - Chebyshev I, HP Filter 36dB/oct (subsonic/rumble filter) @ 20Hz / BW20
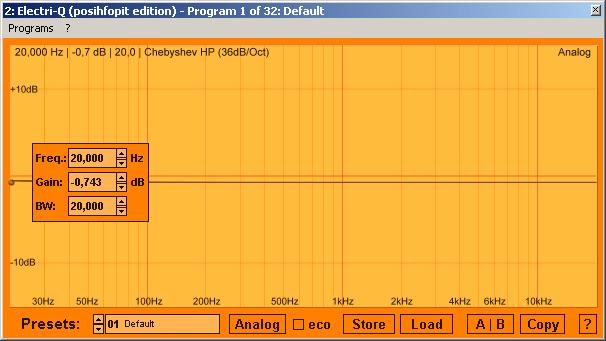
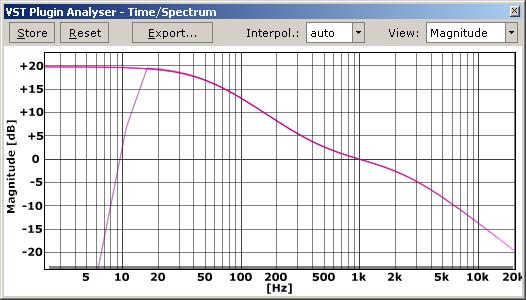
Result (lighter line)
Christian W. Buddes RubberFilter - (48dB/oct @ 20Hz)
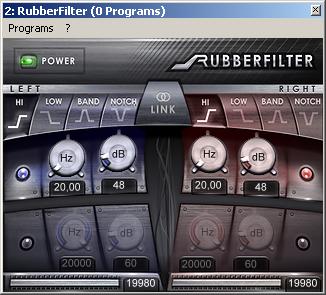
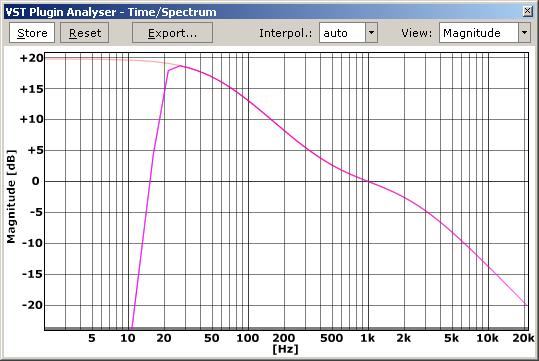
Result:
Both mentioned plug-ins can be found @ http://www.savioursofsoul.de/Christian/?page_id=64
RIAA Filter software specs
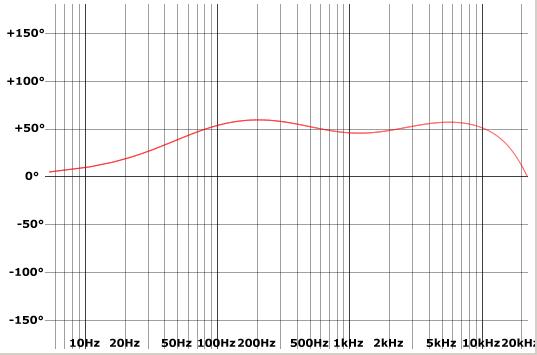
Phase
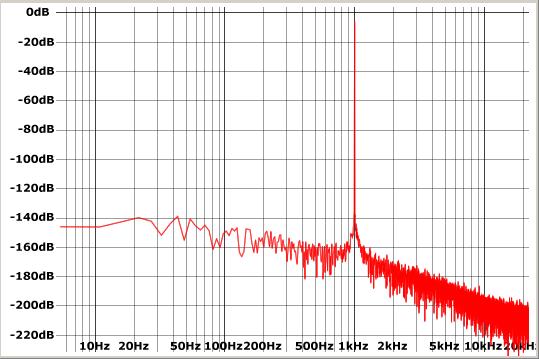
Harmonic distortion
Filter Background (regarding coefficients)
This RIAA Filter accuracy depends on sample-rate because of the filter is sample accurate.
By calculated results (by Robert Orban),
--> the filter should be accurate compared to RIAA standard (* see notes below).
Robert Orban, person behind these filter coefficients, describes the method he used for to calculate coefficients:
An IIR simulation of the RIAA phono de-emphasis curve (assuming s-plane poles at 50.5 and 2122 Hz
and an s-plane zero at 500.5. Hz), here are some good minimum-phase magnitude approximations.
(The RIAA de-emphasis is minimum-phase in the analog domain.
@ 44.1 kHz:
two pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.2239207dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 30 degrees
where the "phase error" is computed after a constant delay is added
or subtracted to make the phase error equiripple
three pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0113530dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 23 degrees
four pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0005780dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 21 degrees@ 48 kHz:
two pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.1395898dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 24 degrees
Three pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0037544dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 16 degrees
four pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0000998dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 15 degrees@ 88.2 kHz
two pole IIR filter
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0081862dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 3 degrees
three pole IIR filter
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0000096dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 2 degrees
etc.@ 96 kHz:
two pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0057028dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 2.4 degrees
three pole IIR filter:
MAXIMUM ERROR FROM 0.00 Hz TO 20000.00 Hz IS 0.0000046dB
MAXIMUM PHASE ERROR FROM 0.00 Hz TO 20000.00 Hz IS ~+/- 1.6 degrees
etc.
-
Given a desired magnitude response in the z-plane, there exists a
response in a frequency-warped u-plane that, when bilinear-transformed
to the z-plane, creates the desired z-plane magnitude response. -
Compute the [magnitude response]^2 of the s-plane prototype on a grid.
This is the square of the desired z-plane response. -
Warp the frequency axis by using the bilinear transform, recognizing
that we are approximating using omega^2 as our frequency variable. The
warp maps Nyquist to infinity. -
Make a least-squares rational approximation (i.e., ratio of
polynomials) to the values on the frequency grid. (I used the Numerical
Recipes routine RATLSQ, which uses Chebychev polynomials.) -
Refine the approximation to make the fractional error minimax by using
Remez's Second Algorithm [which applies to rational functions; it's not
the same as the Remez algorithm used in the classical MPR FIR design
program; see Forman S. Acton, Numerical Methods That Work (Revised
Edition), Washington D.C., American Mathematical Society, 1990, pp 310-
314] -
Transform the result into the z-plane in two steps. The first
recognizes that we have been approximating using the magnitude square
function, so we must take the square roots of the poles and zeros of the
approximated rational function, taking the negative real parts to
guarantee a stable, minimum-phase function. The second step is to apply
the bilinear transform to the result of the first step. This yields the
final z-plane poles and zeros.
There are some "interesting" numerical issues in making this procedure
work, mainly because the Remez update formulas require solving a system
of mildly nonlinear equations that tend be ill-conditioned.
The nice thing about the algorithm is that the frequency-warping moves
Nyquist to infinity and thus increases the resolution of the
approximation close to Nyquist, which is where difficulties often occur.
UPDATES:
04/2010
Scott Wurcer informed me about possible *) error in Orban's calculations and this was confirmed later by Orban.
Orban had used value of 50.5 Hz instead of 50.05 Hz for one pole.
By the given information, resulting error in frequency responce isn't meaningful since it mostly touches lower frequencies. It certainly degrades the overal accuracy mentioned earlier (I have not compared this yet). Instead of fixing coefficients, I'll add another coefficients for 96kHz (see next update).
05/2010
Scott Wurcer presented new 96hHz and 192kHz filter coefficients.
These are calculated using equal height minimum ripple fit (20Hz to 20kHz).
The fit at 192kHz is .00033dB and at 96kHz it is .0056dB.
RIAA EQ filter coefficients (2nd order filter)
To use with software as like SynthMaker, SynthEdit and Max/MSP, etc. on Biquad -implementations.
|
|
FROM CALCULATION (GAINED) |
MATCHED GAIN (~0dB @ 1 kHz) | |||||||||||
|
Coeff Khz |
b0 |
b1 |
b2 |
a0 |
a1 |
a2 |
Gain dB |
b0 |
b1 |
b2 |
a0 |
a1 |
a2 |
|
44.1 |
1.0 |
-1.700724 |
0.7029382 |
1.0 |
-0.7218922 |
-0.1860521 |
+12.466 |
1.0 |
-1.700724 |
0.7029382 |
0.2380952 |
-0.1718791 |
-0.0442981 |
|
48 |
1.0 |
-1.732766 |
0.7345534 |
1.0 |
-0.7555521 |
-0.1646257 |
+12.752 |
1.0 |
-1.732766 |
0.7345534 |
0.0267592 |
-0.0459208 |
-0.0192123 |
|
88.2 |
1.0 |
-1.855465 |
0.8559721 |
1.0 |
-0.8479577 |
-0.1127632 |
+17.944 |
1.0 |
-1.855465 |
0.8559721 |
0.3414135 |
-0.2895042 |
-0.0384989 |
|
96 |
1.0 |
-1.866608 |
0.8670383 |
1.0 |
-0.8535331 |
-0.1104595 |
+18.625 |
1.0 |
-1.866608 |
0.8670383 |
0.1711450 |
-0.1460779 |
-0.0189046 |
|
96 |
1.0 |
-1.866634 |
0.8670602 |
1.0 |
-0.8535323 |
-0.1104603 |
+15.641 |
1.0 |
-1.866634 |
0.8670602 |
0.1170960 |
-0.0999452 |
-0.0129345 |
|
192 |
1.0 |
-1.931263 |
0.9313725 |
1.0 |
-0.8796912 |
-0.1023703 |
+24.350 |
1.0 |
-1.931263 |
0.9313725 |
0.0606061 |
-0.0533146 |
-0.0062043 |
NOTES:
Filter gain can be adjusted by dividing/multiplying Gain coefficients a0, a1, a2 using equal value (i.e. a0/7.5, a1/7.5, a1/7.5 or a0*5, a1*5, a2*5) !!! Do not change b1, b2.
By swapping the a1<->b1 and a2<->b2 you'll get the production filter. This can't be done for matched coefficients!
---------------------------------------------------------------------------------------------------------------------------------
CD Pre-/De-emphasis filter (ISO 908)
Updated 22.8.2011
Instructions:
Needed software:
-
SynthEdit (demo or commercial version) - http://www.synthedit.com/
-
Dave Haupt's Biquad filter module http://www.dehaupt.com/SynthEdit/DH_BiquadFilter.htm
-
Filter project file – https://docs.google.com/file/d/0B2orKJuZJ5YOWlRTblFhWHV0bzA/edit?usp=sharing
-
VST compatible software for to use the plug-in
-
Coefficients - http://sox.sourcearchive.com/documentation/13.0.0/deemph_8h-source.html
Work flow:
Install SynthEdit
Unzip DH module into folder named as modules (default path = SynthEdit install path\modules )
Download SynthEdit project file ISO908Filter_Unset.zip and unzip it into Projects folder (location = SynthEdit install path\Projects)
Start EynthEdit and set file locations
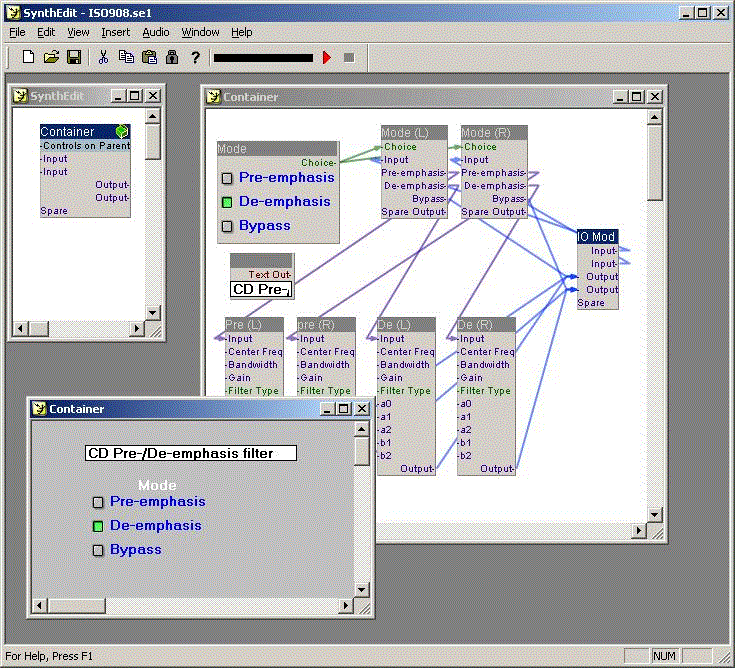
Open the filter project file (ISO908Filter(Unset).se1).
Something like this should show up:
Prepare filters (L/R separately)
Open each Biquad module by activating the module and selecting Properties (menu showen by pressing right-mouse-button).
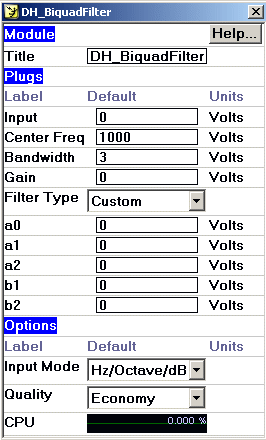
Set the filter type to custom.
Add original coefficients listed @ sox site (link listed earlier) for de-emphasis filter.
De (L) and De (R) modules
Order of coefficients in Biquad module:
a0 = b1_original
a1 = b0_original
a2 = 0
b1 = a1_original
b2 = 0
(save is done by closing the biquad module window)
and then prepare pre-emphasis filters.
First calculate new coefficients so the filter gain is OK.
This is done by multiplying original coefficients a1_original, b0_original and b1_original using 1/b0_original as multiplier.
a1_new = a1_original * 1/b0_original
b0_new = b0_original * 1/b0_original
b1_new = b1_original * 1/b0_original
Multiply b0_new second time using same multiplier.
b0_new = b0_new * 1/b0_original
Pre (L) and Pre (R) modules
Coefficients and order in Biquad module:
a0 = b0_new
a1 = a1_new
a2 = 0
b1 = b1_new
b2 = 0
(save is done by closing the biquad module window)
Sox's Deemph.h includes data for to calculate ideal de-emphasis filter.
Ideal curve filters can be prepared using same logic as used with fitted curve filters.
Save the project.
Compile VST plug-in by selecting ”Save As VST...” (File menu option).
To check if the filter is OK, download and install the Christian Budde's
VST Plugin Analyser - http://www.savioursofsoul.de/Christian/programs/measurement-programs/
Measures:
Sources:
http://en.wikipedia.org/wiki/Pre-emphasis
http://en.wikipedia.org/wiki/De-emphasis
http://www.termwiki.com/IT:CD_emphasis